Interaction models and simulation algorithm¶
PENELOPE combines numerical and analytical total and differential cross sections (DCS) to describe the different interaction mechanisms. These cross sections are the result from approximate physical models and, therefore, are affected by systematic uncertainties. In particular, the DCSs in the database correspond to interactions with free, isolated atoms. DCSs for compounds and mixtures are derived by using Bragg’s additivity rule, i.e., the molecular DCS is approximated by the sum of atomic DCSs of the atoms in a molecule. Aggregation effects are therefore disregarded. These effects are known to be appreciable, e.g. for elastic scattering of electrons with energies less than about 1 keV. Aggregation also affects the photoelectric cross section, causing extended x-ray absorption fine structure effects. On the other hand, the adopted x-ray energies and transition probabilities of excited atoms with inner-shell vacancies pertain to free atoms with a single vacancy. Nonetheless, the structure of the code is flexible enough to enable the use of alternative, more elaborate physical models.
The interaction mechanisms considered in PENELOPE, and the corresponding DCSs, are the following:
- Elastic scattering of electrons and positrons: numerical DCSs obtained from Dirac partial-wave analysis for the electrostatic potential derived from Dirac-Fock atomic electron densities, with the exchange potential of Furness and McCarthy for electrons. These cross sections were calculated using the program ELSEPA [1].
- Inelastic collisions of electrons and positrons: Born DCS obtained from the Sternheimer-Liljequist generalised oscillator strength model [2] [3], including the density-effect correction. Optionally, the DCS can be renormalised to reproduce the collision stopping power read from the input file.
- Electron impact ionisation: numerical total cross sections for ionisation of atomic electron shells obtained from a combination of the distorted-wave Born approximation and the plane-wave Born approximation. The database was computed using the theory and numerical methods described by Bote and Salvat (2008) [4]. These ionization cross sections are much more accurate than those used in older versions of PENEPMA, especially in the energy range of interest in EPMA.
- Bremsstrahlung emission by electrons and positrons: the energy of the emitted photons is sampled from numerical energy-loss spectra derived from the scaled cross-section tables of Seltzer and Berger (1985) [5], optionally renormalised to reproduce the radiative stopping power read from the input file. The intrinsic angular distribution of emitted photons is described by an analytical expression—an admixture of two “boosted” dipole distributions [6]—with parameters determined by fitting the benchmark partial-wave shape functions of Kissel, Quarles and Pratt (1983) [7].
- Positron annihilation: Heitler DCS for two-photon annihilation in flight.
- Coherent (Rayleigh) scattering of photons: Born DCS with an analytical atomic form factor.
- Incoherent (Compton) scattering of photons: DCS calculated using the relativistic impulse approximation with analytical one-electron Compton profiles [8].
- Photoelectric absorption of photons: total atomic cross sections and partial cross sections for the K-shell and L- and M- subshells from the LLNL Evaluated Photon Data Library [9]. The initial direction of photoelectrons is sampled from Sauter’s K-shell hydrogenic DCS.
- Electron-positron pair production: total cross sections obtained from the XCOM program of Berger and Hubbell (1987) [10]. The initial kinetic energies of the produced particles are sampled from the Bethe–Heitler DCS, with exponential screening and Coulomb correction, empirically modified to improve its reliability for energies near the pair-production threshold.
Particle tracks are simulated from the initial energy down to the absorption energies selected by the user, at which particles are considered to be effectively absorbed in the medium. Secondary particles emitted with initial energy larger than the corresponding absorption energy are simulated after completion of each primary track. Secondary particles are produced in direct interactions (inelastic collisions, bremsstrahlung emission, positron annihilation, Compton scattering, photoelectric absorption and pair production) and as radiation (characteristic x-rays and Auger electrons) following inner-shell ionisation. PENELOPE simulates the emission of characteristic x-rays and Auger electrons that result from vacancies produced in K-shells and L- and M-subshells by photoelectric absorption and Compton scattering of photons and by electron or positron impact. The relaxation of these vacancies is followed until all vacancies have migrated to N and outer shells. The adopted transition probabilities have been extracted from the LLNL Evaluated Atomic Data Library [11].
The simulation of photon tracks follows the usual detailed procedure, i.e., all
the interaction events in a photon history are simulated in chronological order.
Electrons can also be simulated in detail, or alternatively, by using a mixed
(class II) simulation algorithm [12].
Mixed simulation algorithms are useful when the electrons undergo a very large
number of interactions and detailed simulation becomes impractical (e.g., for
primary electron energies above 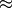 100 keV).
In a mixed algorithm, the user defines cut-off values of the polar scattering
angle (
100 keV).
In a mixed algorithm, the user defines cut-off values of the polar scattering
angle (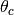 ) and the energy loss (
) and the energy loss (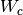 ) in single
interactions.
Hard interactions, with scattering angle
) in single
interactions.
Hard interactions, with scattering angle 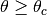 or energy
loss
or energy
loss 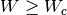 , are simulated individually according to the adopted
single-scattering DCSs.
These interactions are responsible for large lateral displacements or
large energy-loss fluctuations, which detailed simulation describes
faithfully.
The rest of interactions, with
, are simulated individually according to the adopted
single-scattering DCSs.
These interactions are responsible for large lateral displacements or
large energy-loss fluctuations, which detailed simulation describes
faithfully.
The rest of interactions, with 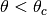 and
and 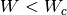 ,
are classified as soft interactions; they have a mild effect on the electron
trajectories and are simulated by using simple, but still fairly accurate,
multiple scattering approximations.
With a judicious selection of the cut-off parameters
,
are classified as soft interactions; they have a mild effect on the electron
trajectories and are simulated by using simple, but still fairly accurate,
multiple scattering approximations.
With a judicious selection of the cut-off parameters 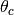 and
and
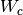 , mixed simulation algorithms yield reliable results in moderate
computation times, even for electrons with very high energies.
, mixed simulation algorithms yield reliable results in moderate
computation times, even for electrons with very high energies.
The straight simulation of EPMA spectra may be very inefficient, even when using mixed simulation algorithms for electron transport. The reason is that the two processes leading to the emission of x-rays (inner-shell ionisation and bremsstrahlung emission) occur with exceedingly small probabilities. That is, on average, we need to generate many electron histories to obtain one emerging photon. Moreover, as the solid angle subtended by the detector is usually very small, only a tiny fraction of the emerging photons hits the detector and contributes to the spectrum. The method adopted in PENEPMA to cope with this difficulty is to use the variance-reduction technique of interaction forcing (also known as the method of weights), which consists of artificially increasing the probability of inner-shell ionisation and bremsstrahlung emission and, at the same time, assigning appropriate statistical weights to the generated secondary particles in such a way that the simulation results remain unbiased. Interaction forcing is also advantageous in studies of fluorescence corrections; in this case the interactions that should be forced are photoelectric absorption and Compton scattering of photons. PENELOPE includes a flexible implementation of interaction forcing, which allows x-ray spectra to be computed in reasonable times (of the order of 1 hour, on modest personal computers).
Notice that PENELOPE tracks primary electrons and all generated particles (electrons and photons), that is, it generates the whole electron-photon shower produced by each primary electron. Therefore, fluorescence effects are consistently described.
The practical usefulness of Monte Carlo simulation lies in its ability to
handle complex geometrical structures.
PENELOPE contains the subroutine package PENGEOM which automatically tracks
particles through arbitrary material systems consisting of homogeneous bodies
limited by quadric surfaces.
Limiting surfaces can be specified either through their implicit equation,
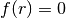 , or by means of their reduced form and a few simple geometrical
transformations.
A quadric surface divides the space into two exclusive regions; the region
where
, or by means of their reduced form and a few simple geometrical
transformations.
A quadric surface divides the space into two exclusive regions; the region
where 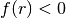 (
(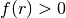 ) is assigned the side pointer -1 (+1).
A body is defined by giving its limiting quadric surfaces and corresponding
side pointers.
Previously defined bodies can be used to define new bodies.
To speed up the geometry operations, the bodies of the material system may be
grouped into modules (connected volumes, limited by quadric surfaces that
contain one or several bodies), which in turn can form part of larger modules.
This modular structure permits a substantial reduction of the work of the
geometry routines, and allows very complicated structures to be considered (the
current version of PENGEOM can handle systems with up to 9,999 surfaces and
5,000 bodies and modules).
Repetitive structures can also be easily defined by using the “clone” operation.
) is assigned the side pointer -1 (+1).
A body is defined by giving its limiting quadric surfaces and corresponding
side pointers.
Previously defined bodies can be used to define new bodies.
To speed up the geometry operations, the bodies of the material system may be
grouped into modules (connected volumes, limited by quadric surfaces that
contain one or several bodies), which in turn can form part of larger modules.
This modular structure permits a substantial reduction of the work of the
geometry routines, and allows very complicated structures to be considered (the
current version of PENGEOM can handle systems with up to 9,999 surfaces and
5,000 bodies and modules).
Repetitive structures can also be easily defined by using the “clone” operation.
- Salvat, F., Jablonski, A., & Powell, C. (2005). ELSEPA}-{Dirac partial-wave calculation of elastic scattering of electrons and positrons by atoms, positive ions and molecules. Comput. Phys. Commun., 165, 157-190.
- Liljequist, D. (1983). A simple calculation of inelastic mean free path and stopping power for 50 {ev}--50 keV electrons in solids. J. Phys. D: Appl. Phys., 16, 1567-1582.
- Sternheimer, R. (1952). The density effect for the ionization loss in various materials. Phys. Rev., 88, 851-859.
- Bote, D., & Salvat, F. (2008). Calculations of inner-shell ionization by electron impact with the distorted-wave and plane-wave born approximations. Phys. Rev. A, 77, 042701.
- Seltzer, S., & Berger, M. (1985). Bremsstrahlung spectra from electron interactions with screened atomic nuclei and orbital electrons. Nucl. Instrum. Meth. B, 12, 95-134.
- Acosta, E., Llovet, X., & Salvat, F. (2002). Monte carlo simulation of bremsstrahlung emission by electrons. Appl. Phys. Lett., 80, 3228-3330.
- Kissel, L., Quarles, C., & Pratt, R. (1983). Shape functions for atomic-field bremsstrahlung from electrons of kinetic energy 1-500 keV on selected neutral atoms 1 < Z < 92. At. Data Nucl. Data Tables, 28, 381-460.
- Brusa, D., Stutz, G., Riveros, J., Fernández-Vera, J., & Salvat, F. (1996). Fast sampling algorithm for the simulation of photon compton scattering. Nucl. Instrum. Meth. A, 379, 167-175.
- Lawrence Livermore National Laboratory. (1989). Tables and graphs of photon-interaction cross sections from 10 eV to 100 GeV derived from the LLNL evaluated photon data library ({epdl}). Livermore, CA: Cullen, D., Chen, M., Hubbell, J., Perkins, S., Plechaty, E., Rathkopf, J., & Scofield, J. .
- National Bureau of Standards. (1987). {xcom}: Photon cross sections on a personal computer. Gaithersburg, MD: Berger, M., & Hubbell, J. .
- Lawrence Livermore National Laboratory. (1991). Tables and graphs of atomic subshell and relaxation data derived from the LLNL evaluated atomic data library ({eadl}), Z=1-100. Livermore, CA: Perkins, S., Cullen, D., Hubbell, J., Rathkopf, J., & Scofield, J. .
- OECD/NEA Data Bank. (2006). {penelope}-2006: A code system for Monte Carlo simulation of electron and photon transport. Issy-les-Moulineaux, France: Salvat, F., Fernández-Vera, J., & Sempau, J. .